ASAB – ciągi podważające dowody Cantora! Czas wyzdrowieć!

Dostatecznie bogaty alfabet pozwala stworzyć przeliczalny zbiór tekstów zawierających wszystkie prace matematyczne, które jak wiemy, mogą nieraz zawierać bardzo wymyślne znaki. Teksty te mogą zawierać także, oprócz twierdzeń, dowodów i definicji matematycznych także dowolne inne teksty, w tym najwyższego gatunku poezję, beletrystykę i fantastykę obok słowników i encyklopedii przemieszanych z przytłaczającą większością tekstów całkowicie bezsensownych. W dodatku mogą to być teksty dawno napisane i zaginione, teksty aktualnie dostępne w postaci książek, plików, jak i teksty, które dopiero powstaną w przyszłości – np. teksty, które Wy napiszecie w odpowiedzi na ten artykuł.

            Często, mimo pozorów sensowności i prawdziwości teksty są z gruntu fałszywe, jak np. „szesnastościan foremny”, lub uznawane za prawdziwe w jednej epoce, a w innym czasie za fałszywe jak: „ciała palne zawierają floginston uwalniany z nich przy spalaniu”. Ocena niektórych tekstów zawsze będzie subiektywna, a w matematyce wolelibyśmy posługiwać się tylko takimi, których interpretacja będzie jednoznaczna. Ale do opisu wielu pojęć matematycznych często stosowany jest metajęzyk, dla którego prawdziwości, jak w przykładzie: „to zdanie jest fałszywe” nie jesteśmy w stanie określić. Automatyczny i bezdyskusyjny wybór wszystkich tekstów o żądanych cechach, w związku z powyższymi uwagami, staje się także trudny do zrealizowania.  A zwłaszcza dla tekstów definiujących wszystkie podzbiory liczb naturalnych, czy też liczby rzeczywiste, co według Cantora, jest w ogóle niemożliwe. Jego dowód i metoda przekątniowa powinna jednak działać dla każdego ciągu odpowiedniego typu i zawsze generować nowe elementy niezawarte w badanym ciągu. Zbadajmy parę ciągów tekstowych, do których arbitralnie wybiorę teksty mające definiować  podzbiory liczb naturalnych zgodne z aktualnymi aksjomatami oraz formułami stworzonymi przez Cantora.    

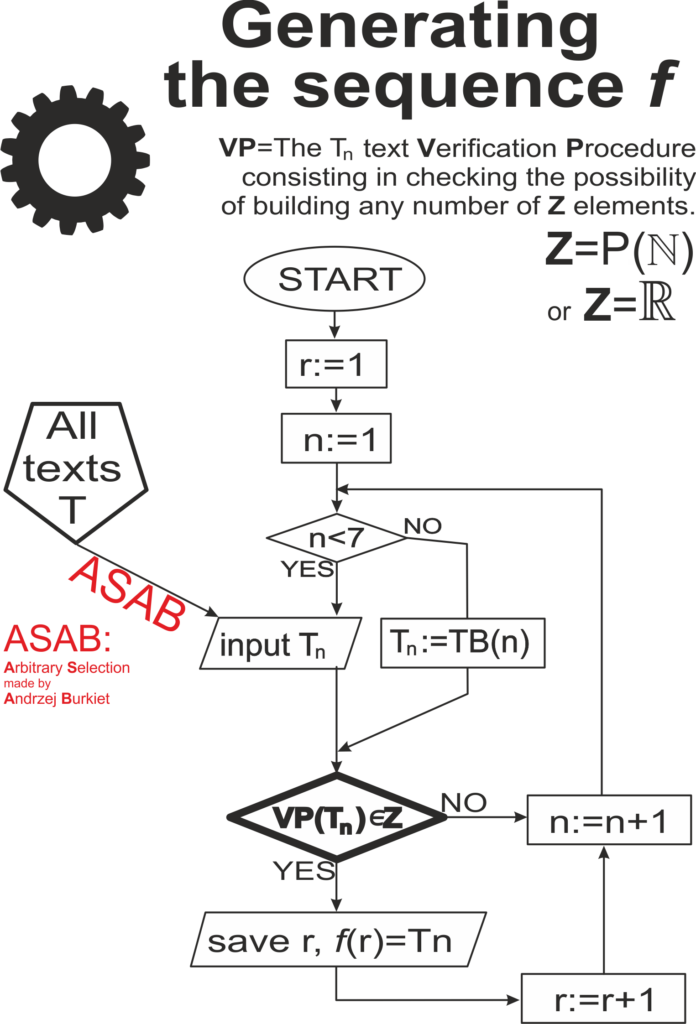
  Poniżej przedstawiam sposób konstruowania takiego ciągu.  Jeśli za kryterium doboru tekstów weźmiemy konieczność definiowania przez tekst podzbioru liczb naturalnych, to powstający ciąg f₁ , będący obrazem arbitralnie wybranego zbioru tekstów ASAB po przejściu procedury weryfikacyjnej VP według załączonego schematu, będzie funkcją f₁:ℕ∋r→T_r≝x_r∈P(ℕ) tych samych tekstów, co w ciągu ASAB, tylko być może w mniejszej ilości, bo bez tekstów wadliwych: T∋ASABx→f₁∈T

  _gdzie T_{-zbiór wszystkich tekstów, ASABx=(T1,T2,..Tn)- arbitralnie wybrany ciąg tekstów z T,} 

  _zaś T_{r- tekst definiujący} x_{r podzbiór liczb naturalnych.}

Procedura VP polega na weryfikacji, czy teksty Ti, zebrane w ciągu ASABx prawidłowo definiują generowane elementy (liczby naturalne zawarte w podzbiorach, lub kolejne cyfry rozwinięcia dziesiętnego liczb rzeczywistych).

            Arbitralnie wyznaczam  ASAB1, czyli następujące teksty, jako kandydatów na wyrazy ciągu f₁:

T₁:          Φ

T₂:          ℕ∖{6,7,8}

T₃:         {x∈ℕ,x∈f₁(x)}

T₄:         {x∈ℕ,x∉f₁(x)}

T₅:  tu wstaw swój pierwszy tekst

T₆:  tu wstaw swój drugi tekst

            I na tym kończę listę tekstów, które mogą tworzyć ten ciąg skończony, czyli zawierający na początku najwyżej sześć wyrazów. A ile naprawdę z powyższych tekstów definiuje podzbiory ℕ?

   Ad1.         Zbiór pusty {} przedstawiony symbolem Φ jest oczywiście podzbiorem ℕ, a zatem

f₁(1)=Φ.

Ad2. Różnica zbiorów ℕ∖{6,7,8} prezentowana w drugim tekście jest również podzbiorem i elementy tego podzbioru możemy przedstawić procedurą VP, jako zbiór nieskończony ASAB1(2)≝{1,2,3,4,5,9,10,11,12,13,14,15,16,…}, gdzie trzykropek symbolizuje następujące po sobie bezpośrednio kolejne liczby naturalne, czyli

f₁(2)= ℕ∖{6,7,8}

Ad3. Co z trzecim tekstem? Sprawdźmy: 1∉Φ=f₁(1), czyli gdyby ten tekst dobrze definiował podzbiór ℕ, to 1∉f₁(3).

Ale z kolei 2∈f₁(2), czyli 2∈f₁(3) i powstający podzbiór zaczynałby się tak: {2,

A co dalej? Czy 3∈f₁(3)? Nie widać przeszkód i wtedy ten definiowany zbiór przez trzeci tekst rozpoczynałby się następująco: {2,3,

A co by było, gdyby jednak 3∉f₁(3)? Tak też może być, tylko wtedy w definiowanym zbiorze nie może się pojawić 3: {2,3,

Skoro to jednak nie jest jednoznacznie określone, bo tekst z tej trzeciej pseudodefinicji {x∈ℕ,x∈f₁(x)}=ASAB1(3) nie precyzuje czy 3 należy, czy też nie należy do generowanego „subciągu”, bo spełnia tę formułę zarówno należąc jak i nie należąc do definiowanej klasy, to musimy ten tekst odrzucić z tworzonego ciągu, jako tekst nie spełniający kryterium VP, który stanowi, że do ciągu można włączyć tylko te teksty, które jednoznacznie definiują elementy podzbioru ℕ. Czyli f₁(3)≠ASAB1(3) i na kandydata do pozycji  nr 3 do ciągu f₁ awansuje zatem następny tekst z ASAB1.

   Tekst czwarty stanowi sformułowanie uzupełniające do tekstu trzeciego, więc skoro tamten tekst nie jest prawidłową definicją zbioru, to możemy się spodziewać, że i ten tekst będzie wadliwy.

Ale sprawdźmy to na wszelki wypadek.

1∉Φ=f₁(1) czyli, gdyby ten czwarty tekst dobrze definiował podzbiór ℕ, to 1∈f₁(3) i zbiór powinien się rozpoczynać f₁(3)≝{1,

Z kolei 2∈{1,2,3,4,5,9,10,11,…}≝f₁(2), a zatem 2 nie może należeć do generowanego zbioru.

Zobaczmy, czy 3 spełnia tę formułę  {x∈ℕ,x∉f₁(x)}:

 Jeśli 3∈f₁(3), to zgodnie z powyższą formułą 3 nie może należeć do generowanego zbioru, natomiast gdyby 3∉f₁(3), to wtedy właśnie element 3 powinien do niego należeć. Sprzeczność.

Ta formuła {x∈ℕ,x∉f₁(x)} nie jest prawidłową definicją zbioru, ponieważ rozważając element równy indeksowi ciągu dochodzimy do sprzeczności. Tekst z pozycji czwartej, podobnie jak poprzedni również musi być wyrzucony z tworzonego ciągu f₁  i zawiera tylko dwa wyrazy: f₁(1)=Φ oraz f₁(2)=ℕ∖{6,7,8}

Formuły {x∈ℕ,x∉f₁(x)} użyto w dowodzie Cantora jako definicji zbioru B, który to zbiór powinien istnieć dla dowolnego ciągu podzbiorów, a tymczasem, jak pokazuję powyżej, już dla prostego ciągu skończonego, formuła ta, z powodów autoreferencyjnych, takiego zbioru nie definiuje dla rozpatrywanego ciągu, jak również nie definiuje zbioru formuła uzupełniająca  {x∊ℕ,x∊f₁(x)} i obie muszą zostać odrzucone z powodu ich autoreferencyjności

       &    &    &

W analogiczny sposób możemy utworzyć skończony ciąg liczb rzeczywistych zdefiniowanych tekstowo f₂ :ℕ∋r→T_r≝x_r∈(0,1)⊂ℝ powstały w wyniku sprawdzania weryfikującego VP polegającego tym razem na wypisywaniu kolejnych cyfr rozwinięcia dziesiętnego liczb(z przedziału (0,1)) zdefiniowanych tekstowo, spośród wybranych arbitralnie tekstów, w postaci ciągu ASAB2 i prowadzącego do zweryfikowanego ciągu : T∋ASAB2→ f₂∈T,

_{gdzie T-zbiór wszystkich tekstów, ASABx- arbitralnie wybrany ciąg tekstów z T, zaś Tr- tekst definiujący liczbę rzeczywistą} x_{r z przedziału (0,1)}

ASAB2:

T₁:     0,5

T₂:     ¾

T₃:  utwórz zapis liczby rzeczywistej wybierając metodą przekątniową cyfry z rozwinięć dziesiętnych liczb zdefiniowanych tekstowo w ciągu f₂

T_4: utwórz zapis liczby rzeczywistej wybierając metodą przekątniową cyfry z rozwinięć dziesiętnych liczb zdefiniowanych tekstowo w ciągu f₂   zamieniając podczas tworzenia cyfry znajdujące się po przecinku na następniki tych cyfr.

                              VP:                    

ASAB2 (1)=0,5      ≝0,5000000000…         f₂(1)=0,5

ASAB2(2)=¾        ≝0,7500000000…         f₂(2)=¾

ASAB2(3)             ≝0,55?

Co tu wstawić zamiast pytajnika? Pasuje każda cyfra, czyli może być zarówno 0,553, 0,559 jak i 0,557 a zatem ten tekst nie określa jednoznacznie liczby (nie wiadomo, czy jest większa od 5/9, czy mniejsza) i należy go skreślić:

        f₂ (3)        =0,55?

Tekst4 różni się od trzeciego końcową operacją, która powinna zmieniać cyfry już wygenerowanej liczby utworzonej z cyfr liczb w ciągu po przekątnej, ale ponieważ tej wcześniejszej nie można utworzyć, więc i dalsze działania jej nie poprawią, choć oczywiście dwie pierwsze cyfry byłyby jeszcze poprawnie określone: 0,66?

Tylko, że tym razem już nie potrafimy zamiast pytajnika ? wstawić żadnej cyfry! Bo jakakolwiek by była, to należy ją zamienić na następnik…

                Stworzyliśmy ciąg dwuwyrazowy definiujący dwie liczby rzeczywiste wykorzystując arbitralnie wskazane przeze mnie teksty.

Jeśli ktoś ma zastrzeżenia do zaproponowanego tekstu metody przekątniowej Cantora, którą odrzuciłem i którą powyżej oznaczyłem kolorem zielonym w tekście4 i zna inną wersję to może ją sobie zmienić, co nie zmieni jej braku kreatywności liczby rzeczywistej.

Powyższe rozumowanie pokazuje, że metoda diagonalna Cantora również zawodzi, nie generując liczb nawet w tak prostych przypadkach. Czyli nie dowodzi nieprzeliczalności liczb rzeczywistych.

Uwaga: Do utworzonych powyżej ciągów można teraz zastosować metody Cantora tworzenia nowych obiektów (podzbiorów oraz liczb rzeczywistych) i nawet dołączyć te obiekty do tych ciągów, ale teksty je tworzące będą albo inne, niż wcześniej rozpatrywane i odrzucone, bo f≠ASAB, albo identyczne z odrzuconymi wcześniej i każda próba ponownego ich dołączenia doprowadzi do powtórnego stwierdzania ich wadliwości przez VP wskutek samoodniesienia.

            Dlaczego zastosowałem powyżej Arbitralną Selekcję tekstów, a nie bardziej ogólny sposób wyselekcjonowania spośród wszystkich tekstów tylko tych, które definiują obiekty danego typu? Takie ogólne ciągi tekstów w sposób wręcz oczywisty zawierać będą te wadliwe teksty z pozycji 3 i 4, ale jest to selekcja bardziej intuicyjna i z formalnego punktu widzenia powstają duże trudności rozróżnienia wszystkich tych tekstów, które dobrze spełniają kryteria doboru i prawidłowo definiują dane obiekty od tych, które są zupełnie podobne do fejkniusów. Dodatkowo często, zanim dotrzemy do tych z pozycji 3 i 4 określonych przy pomocy metajęzyka przez Cantora pewno napotkamy teksty, co do których możemy mieć wątpliwości, czy są prawidłowo napisane i ich ocena może być bardzo subiektywna, a to z kolei zmieniałoby kolejność występowania interesujących nas tekstów stworzonych przez Cantora zależną od interpretacji oceniającego a samo miejsce w szeregu staje się bliżej nieokreślone. Niemniej jednak, tak to już mamy z tym językiem opisowym – czyli tzw. metajęzykiem, że opisuje nie tylko rzeczy i obiekty istniejące naprawdę, ale także, stwarzając pozory prawdy, wierutne bzdury. A teksty Cantora połączone z konstrukcją odpowiednich ciągów są przecież zawarte w zbiorze wszystkich tekstów.

            Stosując bardzo ogólne kryteria wyboru tekstów mających definiować np. podzbiory liczb naturalnych, czy liczby rzeczywiste, lub nawet zbieżny ciąg przedziałów, intuicyjnie jesteśmy pewni, że będą zawierać właśnie te wadliwe teksty Cantora, choć nie wiadomo, na jakiej pozycji, lecz ta niewiedza nie zmieni tego, że zawsze będą przypisane do pewnego indeksu i będą autoreferencyjne, więc powinny być usuwane. Takie ogólne sposoby selekcji znajdziecie w e-booku:

   W tym e-booku (⤒) „INFINITY: END of ALEPH ONE”, dostępnym na Amazonie (po angielsku) oprócz wstępu beletrystycznego (math fantasy), stanowiącego wprowadzenie dla laików, rozprawiam się także z metodą diagonalną Cantora w różnych wersjach, w tym także ze zbieżnym przedziałowo zbiorem Cantora, dowodząc ich fałszywości, opierając się zresztą na podobnym schemacie blokowym selekcji tekstów, jak wyżej zaprezentowany.

            Warto zwrócić uwagę na możliwość dowolnej budowy i rozbudowy ciągów ASAB o kolejne dodawane teksty mające definiować odpowiednie obiekty, czyli także na przykład podzbiory liczb naturalnych lub liczby rzeczywiste i po przejściu odpowiedniej weryfikacji VP tworzyć, także z Waszych tekstów, przeliczalnych zbiorów. Wbrew obowiązującej obecnie narracji, ta przeliczalna nieskończoność tekstów jest bardzo, bardzo pojemna i zawiera nawet obiekty zwane dziś modnie i mylnie streamingami, czyli ciągami zer i jedynek, stosowanymi na przykład w przekazach telewizyjnych, gdzie teoretycznie ciąg ten nie powinien mieć końca, ale niestety ma lub będzie mieć, bo czas każdej transmisji ulegnie zakończeniu wraz z końcem świata…

            Specjaliści od Teorii Mnogości nie mieli dotychczas zastrzeżeń do poprawności opisu metody przekątniowej – sformułowanej przecież metajęzykiem i uważali, że tą metodą zawsze wygenerują nowe obiekty dla każdego ciągu odpowiedniego typu. Stworzone, przy pomocy tego samego metajęzyka, powyższe konstrukcje ciągów udowadniają wadliwość tej metody oraz istnienie ciągów jej niepodlegających, co z kolei pokazuje, że cały gmach Katedry Mnogości wraz z skalą Alefów i wydumaną Hipotezą Continuum stał na glinianych nóżkach egzystencji zbiorów nieprzeliczalnych.

            Ponieważ mamy wolność wyznania wiary, nie będę zabraniać nikomu wierzyć, że mimo wszystko metodą diagonalną można zawsze stworzyć nowe obiekty w nieprzeliczalnej ilości i że w związku z tym istnieją zbiory nieprzeliczalne i całe rodziny liczb kardynalnych.

            Podobnie wobec wolności słowa, zwolennicy Cantorowskich idei mogą oczywiście nadal tworzyć swe dzieła, w które naprawdę wkładają wiele intelektualnego wysiłku, ale ja sam umieszczę je na półce z innymi bajkami i fantastyką opowiadającymi o jednorożcach, smokach, elfach i podróżach z ponadświetlnymi prędkościami poza granice wszechświata i pod horyzont zdarzeń.

Jeśli uważacie, że nie mam racji i istnieją liczby rzeczywiste nie zdefiniowane przez tekst znajdujący się w ciągu AB w książce powyżej i chcecie zarobić 1000.00USD, to szybko kupcie tego e-booka i przyślijcie do mnie swój przepis.

Gdyby wybrane teksty do ciągu ASABx były poprawne, to zastosowana procedura sprawdzająca VP nie powodowałyby odrzucenia żadnego z proponowanych tekstów i 

                                            ASAB = f

       Narzucającym się wnioskiem jest wprowadzenie ograniczalności stosowania aksjomatu podzbioru o formuły autoreferencyjne, bo jak widać sam zakaz stosowania w tych formułach symbolu B (jako symbolu definiowanego zbioru) jest niewystarczający.